Neural network algorithm java implementation

Neural network calculation process

The structure of the neural network is shown in the figure below. The leftmost one is the input layer, the rightmost one is the output layer, and the middle is multiple hidden layers. Each neural node of the hidden layer and the output layer is multiplied by the upper node. It is accumulated by its weight, and the circle marked with "+1" is the intercept term b, and each node outside the input layer: Y=w0*x0+w1*x1+...+wn*xn+b, from which we can know A neural network is equivalent to a multi-layered logical regression structure.

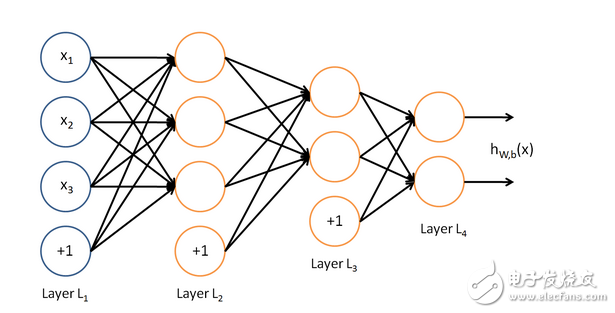
Algorithm calculation process: the input layer starts, calculates from left to right, and proceeds layer by layer until the output layer produces results. If there is a gap between the result value and the target value, then calculate from left to left, calculate the error of each node backwards layer by layer, and adjust the weight of each node. After reaching the input layer in reverse, it will calculate again and repeat. Iterate through the above steps until the ownership weight parameter converges to a reasonable value. Since the computer program solves the equation parameters and the mathematics method is different, generally the parameters are randomly selected first, and then the parameters are continuously adjusted to reduce the error until the correct value is approached. Therefore, most of the machine learning is continuously iterative training. Let us look at the program in detail. It is clear to see the implementation of this process.

Neural network algorithm program code implementation

The algorithm implementation of the neural network is divided into three processes: initialization, forward calculation, and reverse modification of weight.

Initialization process

Since it is an n-layer neural network, we use a two-dimensional array layer to record the node values. The first dimension is the number of layers, the second dimension is the node position of the layer, and the value of the array is the node value. Similarly, the node error value layerErr is also recorded in a similar manner. . The weight of each node is recorded by the layer_weight of the three-dimensional array. The first dimension is the number of layers, the second dimension is the node position of the layer, the third dimension is the position of the lower node, and the value of the array is the weight value of a node reaching a node of the lower layer. The initial value is 0. A random number between -1. In order to optimize the convergence speed, the momentum method is adjusted here. It is necessary to record the last weight adjustment amount, which is recorded by the three-dimensional array layer_weight_delta. The intercept item processing: the intercept value is set to 1 in the program, so only need to calculate it. The weight can be,

2. Calculate the result forward

Use the S function 1/(1+Math.exp(-z)) to unify the value of each node to 0-1, and then calculate it layer by layer until the output layer. For the output layer, it is actually no longer needed. With the S function, we treat the output result as a probability value between 0 and 1, so we also use the S function, which is also conducive to the uniformity of the program implementation.

3. Reverse modification weights

How to calculate the error of the neural network, generally using the squared error function E, as follows:

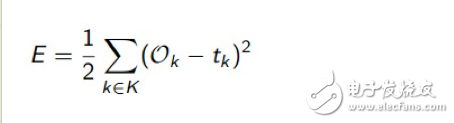
That is, the square of the error of the multiple output items and the corresponding target value is added up and divided by 2. In fact, the error function of logistic regression is also this. As for why this function is used to calculate the error, what is the mathematical rationality, how come it is, I suggest that programmers do not want to be mathematicians, do not go first. After studying it, what we have to do now is how to take the E error of this function to its minimum value, and we need to derive it. If there is some mathematical basis for derivation, we can try to derive how to derive the weight from function E. Get the following formula:

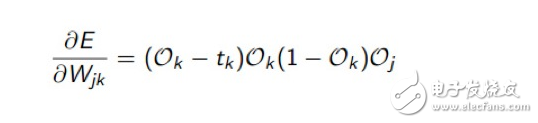
It doesn't matter whether it is deduced or not. We only need to use the result formula. In our program, we use layerErr to record the minimum error of E after deriving the weight, and then adjust the weight according to the minimum error.

Note that the momentum method is used here to take into account the previous adjustment experience and avoid falling into the local minimum. The following k represents the number of iterations, mobp is the momentum term, and rate is the learning step:

There are also a lot of formulas that use the following, the difference in effect is not too big:

In order to improve performance, note that the program implementation is to calculate the error and adjust the weight in a while, first position the position to the penultimate layer (that is, the last layer of the hidden layer), and then adjust the layer by layer, according to L+ The 1st layer calculates the error to adjust the weight of the L layer, and calculates the error of the L layer. It is used to calculate the weight when the next cycle is to the L-1 layer, and the loop is continued until the end of the first layer (input layer).

summary

Throughout the calculation process, the value of the node is changed every time, no need to save, and the weight parameter and error parameter need to be saved, and need to support the next iteration. Therefore, if we conceive a distributed The multi-machine parallel computing solution can understand why there is a Parameter Server concept in other frameworks.

Multi-layer neural network complete program implementation

The following implementation program BpDeep.java can be used directly, and it can be easily modified to any other language implementation such as C, C#, Python, etc., because the basic statements are used, and other Java libraries are not used (except the Random function). The following is the original procedure, please indicate the author and source when reprinting the quote.

Import java.uTIl.Random;

Public class BpDeep{

Public double[][] layer;// neural network nodes

Public double[][] layerErr;// neural network node error

Public double[][][] layer_weight;//each node weight

Public double[][][] layer_weight_delta;//each node weight momentum

Public double mobp;//momentum coefficient

Public double rate;//learning coefficient

Public BpDeep(int[] layernum, double rate, double mobp){

This.mobp = mobp;

This.rate = rate;

Layer = new double[layernum.length][];

layerErr = new double[layernum.length][];

Layer_weight = new double[layernum.length][][];

Layer_weight_delta = new double[layernum.length][][];

Random random = new Random();

For(int l=0;l "layernum.length;l++){

Layer[l]=new double[layernum[l]];

layerErr[l]=new double[layernum[l]];

If(l+1"layernum.length){

Layer_weight[l]=new double[layernum[l]+1][layernum[l+1]];

Layer_weight_delta[l]=new double[layernum[l]+1][layernum[l+1]];

For(int j=0;j"layernum[l]+1;j++)

For(int i=0;i"layernum[l+1];i++)

Layer_weight[l][j][i]=random.nextDouble();//random initialization weight

}

}

}

/ / Calculate the output layer by layer

Public double[] computeOut(double[] in){

For(int l=1;l "layer.length;l++){

For(int j=0;j"layer[l].length;j++){

Double z=layer_weight[l-1][layer[l-1].length][j];

For(int i=0;i"layer[l-1].length;i++){

Layer[l-1][i]=l==1? In[i]:layer[l-1][i];

z+=layer_weight[l-1][i][j]*layer[l-1][i];

}

Layer[l][j]=1/(1+Math.exp(-z));

}

}

Return layer[layer.length-1];

}

/ / Calculate the error layer by layer and modify the weight

Public void updateWeight(double[] tar){

Int l=layer.length-1;

For(int j=0;j"layerErr[l].length;j++)

layerErr[l][j]=layer[l][j]*(1-layer[l][j])*(tar[j]-layer[l][j]);

While(l--》0){

For(int j=0;j"layerErr[l].length;j++){

Double z = 0.0;

For(int i=0;i"layerErr[l+1].length;i++){

z=z+l》0? layerErr[l+1][i]*layer_weight[l][j][i]:0;

Layer_weight_delta[l][j][i]= mobp*layer_weight_delta[l][j][i]+rate*layerErr[l+1][i]*layer[l][j];//implicit layer momentum Adjustment

Layer_weight[l][j][i]+=layer_weight_delta[l][j][i];//implicit layer weight adjustment

If(j==layerErr[l].length-1){

Layer_weight_delta[l][j+1][i]= mobp*layer_weight_delta[l][j+1][i]+rate*layerErr[l+1][i];//Intercept momentum adjustment

Layer_weight[l][j+1][i]+=layer_weight_delta[l][j+1][i];//Intercept weight adjustment

}

}

layerErr[l][j]=z*layer[l][j]*(1-layer[l][j]);//recording error

}

}

}

Public void train(double[] in, double[] tar){

Double[] out = computeOut(in);

updateWeight(tar);

}

}

An example of using a neural network

Finally, we will find a simple example to see the magical effects of neural networks. In order to facilitate the observation of the data distribution, we choose a two-dimensional coordinate data, there are 4 data below, the square represents the data type is 1, the triangle represents the data type is 0, you can see that the data belonging to the block type has (1, 2 ) and (2,1), the data belonging to the triangle type has (1,1), (2,2). Now the problem is that we need to divide the 4 data into 1 and 0 on the plane, and use this to predict the new The type of data.

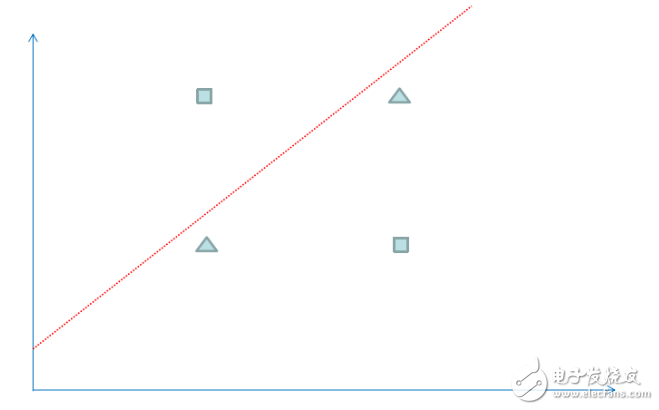
We can use the logistic regression algorithm to solve the above classification problem, but the logistic regression gets a linear line as the dividing line. You can see that the red line above is always placed in a different type regardless of how it is placed. Therefore, for the above data, only one straight line can't divide their classification correctly. If we use the neural network algorithm, we can get the classification effect of the following figure, which is equivalent to multiple straight line summation to divide the space, so the accuracy is more high.

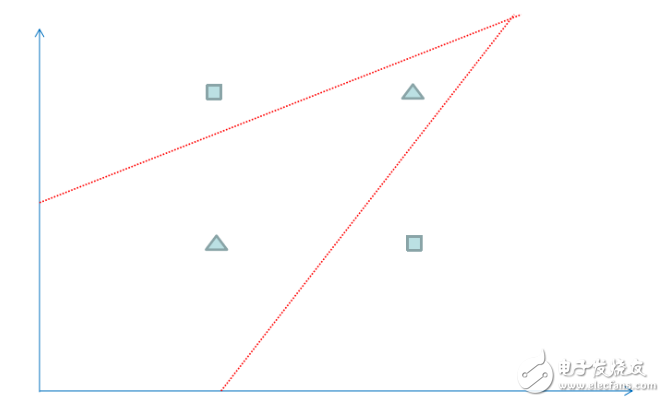
The following is the source code of this test program BpDeepTest.java:

Import java.uTIl.Arrays;

Public class BpDeepTest{

Public staTIc void main(String[] args){

/ / Initialize the basic configuration of the neural network

/ / The first parameter is an integer array, representing the number of layers of the neural network and the number of nodes per layer, such as {3,10,10,10,10,2} means that the input layer is 3 nodes, the output layer is 2 Nodes with 4 hidden layers in the middle, 10 nodes per layer

//The second parameter is the learning step size, and the third parameter is the momentum coefficient.

BpDeep bp = new BpDeep(new int[]{2,10,2}, 0.15, 0.8);

/ / Set the sample data, corresponding to the above four two-dimensional coordinate data

Double[][] data = new double[][]{{1,2},{2,2},{1,1},{2,1}};

/ / Set the target data, corresponding to the classification of 4 coordinate data

Double[][] target = new double[][]{{1,0},{0,1},{0,1},{1,0}};

/ / Iterative training 5000 times

For(int n=0;n"5000;n++)

For(int i=0;i"data.length;i++)

Bp.train(data[i], target[i]);

/ / Test sample data based on training results

For(int j=0;j"data.length;j++){

Double[] result = bp.computeOut(data[j]);

System.out.println(Arrays.toString(data[j])+":"+Arrays.toString(result));

}

/ / Based on the training results to predict the classification of a new data

Double[] x = new double[]{3,1};

Double[] result = bp.computeOut(x);

System.out.println(Arrays.toString(x)+":"+Arrays.toString(result));

}

}

summary

The above test procedure shows that the neural network has a very amazing classification effect. In fact, the neural network has certain advantages, but it is not a versatile algorithm close to the human brain. In many cases, it may disappoint us, and it needs to be combined with data of various scenarios. To observe the effect. We can change the 1 layer hidden layer to n layer, and adjust the number of nodes per layer, the number of iterations, the learning step and the momentum coefficient to get an optimized result. But in many cases, the effect of the n-layer hidden layer is not significantly improved compared to the first layer. Instead, the calculation is more complicated and time-consuming. Our understanding of the neural network requires more practice and experience.

Tile Light Series

LED Tile ligh,Waterproof led tile lamp

Kindwin Technology (H.K.) Limited , https://www.szktlled.com